To develop a full understanding of a concept and its application students must integrate information from multiple perspectives.
When students are taught to investigate a concept from multiple perspectives, they are encouraged to apply different semiotic (meaning-making) resources to a problem. Doing so enables students to view a mathematical problem in different and new ways, and to begin to consider how to apply different mathematical approaches to solve a problem.
For example, for the concept of surface area of a solid, students need to make and discuss the links between:
- the three-dimensional object (or picture of the object)
- its two-dimensional net representation.
This should lead students to be able to construct a formula to calculate surface area.
To support this, students can be given activities that involve multiple representations (e.g. a picture of a solid and its net) for multiple cases (e.g. various solids) (HITS 6: Multiple exposures).
Understanding this strategy
In this strategy:
- students work in pairs or groups on different cases
- each group explains their reasoning on their case to the class.
Looking at a range of cases allows the class to consider similarities and differences between the cases. This strategy also uses
HITS 5: Collaborative learning, and can be used anytime there are individual cases that together help to build a concept.
The example below demonstrates how this strategy can be used in a Year 9 class to support the teaching of surface area formulas (VCMMG313,
VCMMG314).
Example using multiple perspectives to investigate a concept
Problem
Sets of 3 cards need to be prepared before the class, where each set relates to one solid. Colour-coding the cards will help in the activity (i.e. card 1 is colour 1, etc).
- card 1: Picture of the solid with relevant measurements
- card 2: Diagram of the net with relevant measurements
- card 3: Calculations for the surface area
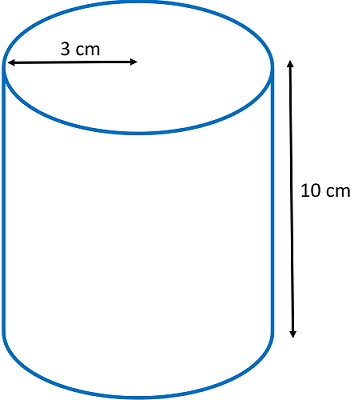Card one: Picture of the solid
with relevant measurements
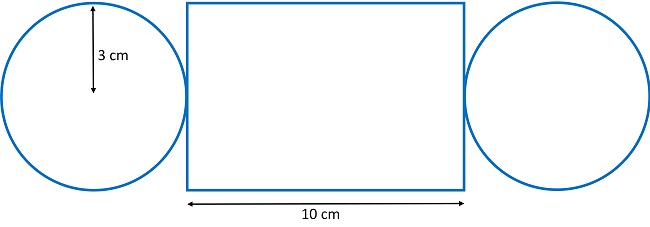
Card two: Diagram of the net with relevant measurements
Card three:
S.A. = 2πr2 + lw
S.A. = 2πr32 + 10(3)
S.A. = 18π + 30
S.A. ≈ 86.5 cm2
Classroom learning
Students are given a card (for example, on entry to the classroom) and instructed to find the other two students with cards relating to that same solid (colour-coding helps here).
The task of each group is to determine how their net (card 2) relates to their solid shape (card 1) and how the surface area calculation (card 3) relates to the other two.
The teacher then shows the first case (solid with net and surface area calculations) to the class and asks the group who worked on that to report on what they noticed. The process is repeated until all cases (i.e., groups) have been considered.
Summary notes could then be created by the class to explain what surface area is and how it is calculated.