Some problems require students to look for a pattern to find a solution. When reading text, students need to learn to identify whether the problem might be solved by considering an initial case.
For example, n = 1, then moving to following cases n = 2, n = 3, and so on.
This requires students to be able to identify that the language used in the problem indicates that a pattern needs to be found. Students can then identify the underlying structure in a solution.
When doing this, students should be encouraged to explain the pattern in words or produce a formula to represent the situation.
Understanding this strategy
To support students to achieve this, teachers can:
- Ask students to discuss which wording suggests that looking for a pattern may be helpful or not helpful in a problem.
- Model the use of systematic recording of data to enable identification of a pattern
- Explain to students that there are two types of formulae: recursive and functional. These are illustrated in the example below. Discuss the advantages and limitations of each type of formula.
The example below is from a Year 7 class on algebra (VCMNA252), and also links to the
Mathematics proficiency 'Understanding', where students have to describe their thinking mathematically (VCAA, n.d.).
Example using a pattern to solve a complex problem
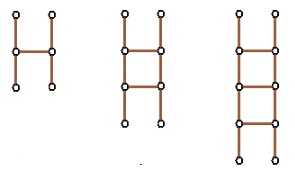 Patterns representing equations
Patterns representing equations Problem
Ladders can be made using equal lengths of metal with joining rings to connect them; some examples are shown below. How many metal pieces would be needed for a ladder with five steps? And for a ladder with thirty steps? And for a ladder with any number (n) of steps?
Sample patterns
In groups, students can discuss which wording suggests that looking for a pattern may be helpful or not helpful in each problem in the set.
Clues in the question include:
- asking for solutions to two different numbers of rungs: 5 and 30
- asking for a solution for n rungs.
Teacher actions
The teacher can model how to gather enough information to answer the first part:
How many metal pieces would be needed for a ladder with five steps?
This is likely to involve drawing the ladder with five steps and counting the 17 metal pieces.
The teacher can then model how to organise the information to look for a pattern; for example, by completing a table.
Example
| n | 1
| 2
| 3
| 4
| 5
|
|---|
|
Number of metal pieces | 5
| 8
|
|
|
|
|---|
Student learning
In groups, students complete tables and look for a pattern, which should (initially) be described in words.
It is likely that several different wordings of the pattern will be suggested; discussion about their equivalence is a valuable activity (either group or whole class).
Describing patterns
The teacher can describe the pattern in two ways as follows:
recursively: start with 5 lengths for the first case with 1 step, and add 3 for every extra steps
functionally: 3 times the number of steps n, and add 2.
Both of these ways to describe the pattern are valid and both can lead to the correct answer of 92 metal pieces for the second part: And for a ladder with thirty steps?
The functional description of the pattern has the advantage that it is more efficient for dealing with larger values for n; the recursive description requires all intermediate cases to be determined – in this problem, from 5 steps to 29 steps.
Using patterns to reason a solution
To answer the third part of the ladder problem, And for a ladder with any number (n) of steps, the recursive and functional relationships are expected to be written symbolically.
- Ask students to try using algebra to write the relationship that they found.
- Collect correct examples for class discussion.
- Discuss with students which form they prefer and why.
- It is important that students write a statement to explain what the letters/pronumerals represent in their formulae.
- In this problem, n is the number of steps, but the number of metal pieces could be any letter; for example, let w be the number of metal pieces.
Solution
As before, the pattern may be described in two ways as follows:
Recursively: w(1) = 5, then w(n+1) = w(n) + 3, or
Functionally: w = 3n + 2.