Mathematics level 10 - Number and algebra

Teaching context - Inverse proportion

Prior to this level, students have solved problems involving direct proportion (VCMNA301). Direct proportion describes a relationship between two variables that increase at the same rate (y ∝ 5 ∝ 5x), or decrease at the same rate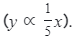

At this level, inverse proportion is introduced and students will discover that as one variable increases the other decreases and vice-versa. Support students to see this relationship by providing examples.

E.g. if a is inversely proportional to b, an equation to represent this is

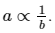
Students will identify inverse proportion in real-life contexts such as the speed of a car, speed = distancetimespeed =

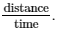Students are successful when they can:

• write a proportion using the variables and (the symbol for proportion)
• write an equation to represent a situation, including k, where k is a constant
• sketch a graph, given a table of values (or other information), identify the shape and state whether or not the relationship is inversely proportional.

A common misconception is that the constant of proportionally (k) is always 1 or simply omitted i.e. students do not include k when setting up an equation.

E.g. given the statement ‘a is inversely proportional to b', students may write 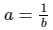rather than

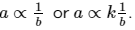
Explain that the proportional sign indicates that what is being solved is part of an equation and therefore cannot have an equal sign. In order to include the equal sign, a constant factor (i.e. k) must be introduced.

Support students by reinforcing the concept of the constant of proportionality and provide these steps to scaffold problem solving:

• Write the proportional relationship using the symbol ∝.
• Convert the proportional relationship into an equation by using a constant of proportionality (k).
• Use the given information to find the constant (k).
• Substitute the constant into the equation.

The next step in this area of learning could be to explore other non-linear relationships proportionalities such as square and inverse square proportions.

Teaching idea - Balancing act

In this hands on activity students will use a metre ruler to find the relationship between balancing distance and weight. Students will use reasoning to determine if there is an inversely proportional relationship or not.

Provide students with metre rulers and ask them to explore what happens when they balance the ruler at the centre point.

Ask students to add a weight to one side of the ruler, keeping the ruler balance. Provide weights of 100 grams, 200 grams, 300 grams, 400 grams and 500 grams for students to explore.

Students use the information gathered to determine whether or not the balancing distance is inversely proportional to the weight. Students may use equations, graphs or other methods to justify their thinking. They may like to create an A3 poster to display their findings, which could be used as a presentation or as a display in class.

Extension ideas
Pre-test students on their inverse proportion knowledge so high-ability students can have their curriculum compacted and extended. High-ability students could be grouped together for this task.

Grouping high-ability students together allow them to work at a similar pace and level of complexity. This creates a greater level of challenge for them as they collaborate on the task.

High-ability students could be asked to investigate examples of other inverse relationships or use their knowledge of inverse relationships to solve problems.

Requiring high-ability students to investigate alternate scenarios, or to use their knowledge and skills in complex situations will support transfer. This will consolidate their learning while also ensuring they are using higher order thinking.