Foundation Level: Trusting the count
Materials:
Instructions:
Bold type indicates what should be said.
Say: “I’m going to show some cards with some black dots, like this.” Show the first card of Set 1 for as long as it takes to mentally count “one and two and” (approximately 2 seconds). “I want you to tell me how many dots there are on each card as quickly as you can”. If child did not say “two” when shown the card, ask them to say how many they saw, then proceed. “If you can’t tell me, that’s okay, we’ll just move on, but I want you to try as hard as you can.”
Show each card in the order listed for approximately 2 seconds starting with the second card from Set 1. Avoid making any comments.
If answered correctly place the card face down on your left (pile A).
If no response or incorrect after 2 seconds (that is, after a count of “one-and-two-and”), place the card face down on your right (pile B) together with any remaining cards and proceed to the next Card Set.
After the student has left, record which cards are in each pile in a table like the one below.
| Student: |
|
Date: |
|---|
Card Set: |
Pile A |
Pile B |
1. Single Digit (2, 4, 5, 8, 10) |
|
|
2. Ten-Frame Doubles (1, 3, 4, 6, 9) |
|
|
3. Ten-Frame To Five (3, 6, 8, 0) |
|
|
4. Ten-Frames Random (2, 4, 5, 7, 10) |
|
|
5. Two Ten-Frames (12, 14, 17, 19) |
|
|
Advice Rubric
Student responses to this task indicate the extent to which they are able to recognise numbers without counting. This ability referred to as subitising, is an essential pre-requisite for establishing part-part-whole number knowledge for the numbers 1 to 10. That is, that 7 can be understood or recognised in terms of 5 and 2, 1 more than 6, 3 and 4, 1 less than 8, 3 less than 10 and so on. This task consists of 5 different card sets. Each set is ordered from smaller to larger numbers. Teachers were advised to stop and proceed to the next set as soon as the student encountered a problem (took longer that 2 seconds to respond or no response given).
| Observed response |
Interpretation/Suggested teaching response |
|---|
Little/no response (eg, identifies first card of each set only), or clearly guessing |
May not understand task, may not know number names, may not recognise small collections
- Provide opportunities to make, count, name and record small collections
- Practice one-to-one counting with appropriate materials using correct number naming sequence
- Support students to read, write and say number names and symbols
|
Consistently recognise numbers up to 5 in 2 seconds or less (pile A), can occasionally recognise some numbers larger than 5 in 2 seconds (pile B) |
Able to subitise numbers to 5
- Check that students trust the count for the numbers up to 5, that is, that they can work with a given number (said or read as a word or numeral) without having to make that number.
- Provide opportunities to count on from hidden, where the collection or numeral hidden is less than/equal to 5 and the number to be counted is represented as a collection
- Develop and consolidate part-part-whole number knowledge for numbers to 5 (eg, 5 is 4 and 1, 2 and 3 etc) then build on this to establish this knowledge for numbers to 10 using ten-frames and counting on from with particular attention to 10
|
Consistently recognises numbers up to 6 in 2 seconds or less (pile A) and most numbers to 10 in less than 2 seconds (pile B), may recognise some teen numbers without counting on by ones |
Able to subitise numbers to 5, suggests part-part-whole knowledge for numbers 1 to 10 generally well established
- Consolidate part-part-whole number ideas to 10 by providing plenty of practice in recognising numbers displayed quickly, use a variety of flash card displays, eg, various ten-frame representations and cards with separate groups such as a 5 and 3, or a 2, 4 and 3, or a 5, 2, 4 and 3 (eg, see the Subitisation Cards (PDF - 50Kb)).
- Build a sense numbers beyond ten by using two ten-frames or recognised representations of a group of 10 (eg, last card in Set 1), encourage students to say, “10 and 4 more, 14”
|
Able to recognise all numbers to 10 in less than 2 seconds and most of remaining cards without counting by ones |
Indicates a well developed capacity to subitise, a sound knowledge of part-part-whole and sense of numbers beyond 10, needs to work on mental strategies for addition to deal with larger numbers
- Use this knowledge to scaffold the count-on-from-larger mental strategy for single digit combinations involving 1, 2 or 3, eg, 2 and 7 presented orally, students count on from 7 saying, 7 … 8, 9 without relying on physical models.
- Once this is established, use a 2-row (2 coloured) bead frame to build a knowledge of doubles facts to 20, eg,
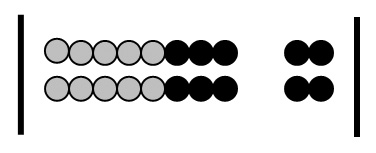
In this case, encourage the thinking: 8 and 8 is 10 and 6 more (refer to visual image), that is, 16
- Work initially with ten-frames and concrete materials to demonstrate the use of part-part-whole knowledge for adding numbers larger than 5, eg, for 6 and 8, start with larger and physically make-to-ten, eg,
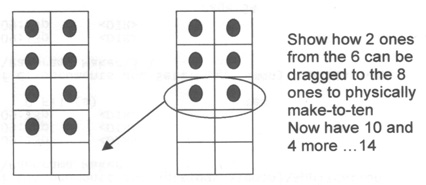
- Extend to working with Open Number Lines (lines with no graduations/markings, this is important as the whole purpose of this is to discourage counting by ones)

Eventually, students should be able to do this mentally. Known as the make-to-ten strategy, this is quite difficult as it involves the simultaneous use of part-part-whole knowledge, in this case, that 8 is 2 less than 10 and 6 is a 2 and a 4 |