The following resources and support materials help teachers build their confidence and capacity to develop and deliver quality teaching and learning programs for numeracy and mathematics and help to improve student outcomes.
The proficiencies in mathematics
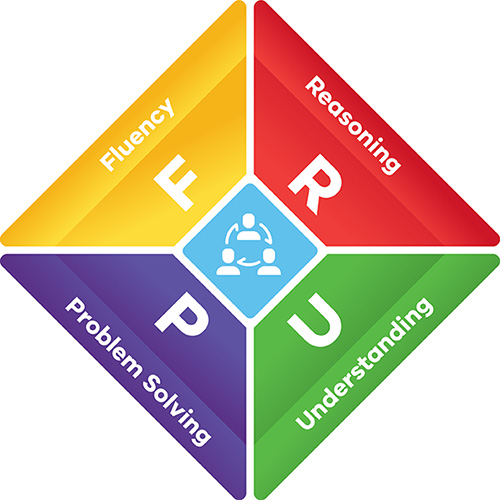
Fundamental to learning mathematics and working mathematically are the four proficiencies of:
- understanding
- fluency
- problem solving
- reasoning.
The proficiencies are applied across the three strands in Mathematics:
- Number and Algebra
- Measurement and Geometry
- Statistics and Probability.
By integrating the four proficiencies you can build capacity and confidence to teach curriculum content, support planning for numeracy, support students to become more independent in their learning and apply their learning and knowledge to solve unfamiliar mathematical problems.
For information on the proficiencies in mathematics see:
Victorian Curriculum F - 10: Learning in Mathematics.
Mathematics teaching practice
Mathematics teaching practice works best when it:
- draws on a range of important mathematical content
- is engaging for students
- caters for a range of levels of understanding
- is successfully undertaken using different methods or approaches
- provides a measure of choice or openness, leading to a sense of student agency
- actively involves students in their own learning
- shows how mathematics can help make sense of the world
- makes appropriate and effective use of technology
- allows students to make connections between the concepts they have learned
- draws students attention important aspects of mathematical activity
- helps teachers decide what help students may need.
(Charles Lovitt and Doug Clarke (2011) A Designer Speaks: The features of a rich and balanced mathematics lesson: Teacher as Designer).
High impact teaching strategies – numeracy and mathematics
High Impact Teaching Strategies (HITS) are 10 instructional practices that increase student learning.
HITS have the strongest impact on children and young people’s learning when embedded into an ongoing improvement cycle.
Each of the HITS in this section is focussed on numeracy, with examples provided in learning areas other than mathematics. They are organised by developmental stage:
See
High Impact Teaching Strategies for more information.
Scaffolding practices
Using a range of scaffolding practices supports students in their learning process and helps teachers make more informed decisions about how they will meet the learning needs of their students.
The scaffolding practices, researched in Victorian primary schools are:
Excavating
drawing out, digging, uncovering what is known, making it transparent
Teacher systematically questions to find out what students know or to make the known explicit. Teacher explores children’s understanding in a systematic way.
Modelling
demonstrating, directing, instructing, showing, telling, funnelling, naming, labelling, explaining
Teacher shows students what to do and/or how to do it. Teacher instructs, explains, demonstrates, tells and offers behaviour for imitation.
Collaborating
acting as an accomplice, co-learner/problem-solver, co-conspirator, negotiating
Teacher works interactively with students on a task to jointly achieve a solution. Teacher contributes ideas, tries things out, responds to suggestions of others, invites comments/opinions in what she/he is doing and accepts critique.
Guiding
cuing, prompting, hinting, navigating, shepherding, encouraging, nudging
Teacher observes, listens, monitors students as they work, asks questions designed to help them see connections, and/or articulate generalisations.
Convince me
seeking explanation, justification, evidence; proving
Teacher actively seeks evidence, encourages students to be more specific. Teacher may act as if he/she doesn’t understand what students are saying, encourages students to explain, to provide/obtain data.
Noticing
highlighting, drawing attention to, valuing, pointing to
Teacher draws students attention to particular feature without telling students what to see/notice (i.e. by careful questioning, rephrasing or gestures), encourages students to question their sensory experience.
Focusing
coaching, tutoring, mentoring, flagging, redirecting, re-voicing, filtering
Teacher focuses on a specific gap (i.e. a concept, skill or strategy) that students need to progress. Teacher maintains a joint collective focus and provides an opportunity for students to bridge the gap themselves.
Probing
clarifying, monitoring, checking
Teacher evaluates students understanding using a specific question/task designed to elicit a range of strategies, presses for clarification and identifies possible areas of need.
Orienting
setting the scene, contextualising, reminding, alerting, recalling
Teacher sets the scene, poses a problem, establishes a context, invokes relevant prior knowledge and experience, provides a rationale (not necessarily at the beginning of the lesson, but at the beginning of a new task/idea).
Reflecting/reviewing
sharing, reflecting, recounting, summarising, capturing, reinforcing, reflecting, rehearsing
Teacher orchestrates a recount of what was learnt, a sharing of ideas and strategies. This typically occurs during whole class share time at the end of a lesson where learning is made explicit, key strategies are articulated, valued and recorded.
Extending
challenging, spring boarding, linking, connecting
Teacher sets significant challenge, uses open-ended questions to explore extent of children’s understanding, facilitate generalisations, provide a context for further learning.
Apprenticing
inviting peer assistance, peer teaching, peer mentoring
Teacher provides opportunities for more learned peers to operate in a student-as-teacher capacity, endorses student/student interaction.
In practice examples
reSolve lesson inquiry
A foundation teacher explains her use of the
reSolve lesson inquiry resources and how to differentiate student learning in a problem-based learning approach. The teacher uses the picture book
'1 is a snail, 10 is a crab’ by April Sayre and Jeff Sayre to engage students in conceptual understanding of place value.
Discussion prompts:
- Which of the four numeracy proficiencies do you see enacted in this practice example?
- How does this activity develop understanding of the key concept of ‘teen numbers’?
- How are the HITs represented in this video?
- In what way does the activity enable a differentiated experience for students?
- Why was the teacher concerned about teaching this concept, and how does her use of this activity link to the practice principles for excellence in teaching and learning?
Number talks at Derrimut Primary School
Number talks are part of the numeracy program at Derrimut Primary School where students can use and develop their receptive and expressive language skills to explain, explore and build their understanding of foundational mathematics concepts.
Discussion prompts:
- Which of the four numeracy proficiencies do you see enacted in this example?
- What forms of assessment do you see being used this video?
- How are the HITs represented in this video?
- How does the example link to the Practice Principles for Excellence in Teaching and Learning?
See our
curriculum planning page for more in practice examples.
Maths through Chinese
The Chinese teacher at Knox Park Primary School incorporates elements of Mathematics in her Chinese language program.
This clip features some examples of how she supports her Year 1/2 students to develop their Numeracy skills through Chinese. Explore these activities on FUSE Maths through Chinese.
Maths through German
Effective teaching of Mathematics through German requires careful planning of both the Mathematics and Language elements.
This clip features a teacher of German demonstrating and reflecting on the way he incorporates High Impact Teaching Strategies (HIT) to inform the planning and teaching of Mathematics through German with Year 3/4 students at Carrum Primary School. Explore these activities on FUSE Maths through German.
Student-centered teaching and learning
Teachers and students discuss the approach to Mathematics at Sunshine College and the positive impact of collaborative learning. This video presents a model of differentiation that is used to enhance student engagement in learning and build confidence and capacity in working with mathematics. Explore these activities on FUSE Student-centred teaching and learning.
Discussion prompts:
- How is student agency represented in this video?
- What are the advantages of using a student centred approach to mathematics learning?
- What is the school’s approach to assessment in mathematics and how does it differ to the approach at your school?
- In your opinion, what is more valuable, assessment of attainment or assessment of growth?
Targeted numeracy intervention in action
St Albans Secondary College explain their
practical approach to supporting students to develop their numeracy. After researching strategies, St Albans decided to carry out the
Getting Ready in Numeracy (GRIN) Intervention Program for a group of students experiencing low learning growth in mathematics in Years 7 and 8.
The program involves teachers providing additional tutoring sessions of 15-20 minutes, three times per week, with small groups of students.
Interactive EAL Effective Practice Guide
This guide offers a
series of videos and discussion prompts highlighting explicit pedagogy for teaching the language and literacy of Mathematics and Science in secondary schools.
The following discussion prompts relate to the videos:
teaching the language and literacy of Mathematics and
oral language in Mathematics.
Discussion prompts
- Reflect on the teacher's use of the HITS.
- Where do you see Mathematics proficiencies in the teacher's practice?
- What types of questions support students to build their reasoning and understanding?
- What element of the teacher's practice might you trial?
Use the discussion prompts below for the video
Breaking down questions in Mathematics
Discussion prompts
- Reflect on use of the Explicit Teaching, Worked Examples and Multiple Exposure HITS.
- Where do you see the Mathematics proficiencies in the teacher's practise?
- Comment on the PowerPoint resource that was used for this lesson and share comments with your colleagues.
- Discuss examples of where your students find it hard to understand and break down questions in Mathematics.
- What elements of the teacher's practice might you commit to trialing?
Resources
References
Educationaldesigner.org (2019)
A Designer Speaks[online]
Files.eric.ed.gov. (2019). [online] Researching numeracy approaches in primary schools (DEST, 2004) researched in Victorian primary schools [Accessed 8 Aug. 2019].