Evidence and research underpin the learning and development in mathematics and numeracy.
Common myths
Being numerate involves using mathematics. Not everyone is confident with mathematics or believes that they can do mathematics.
Research provides clear and compelling evidence that attitudes and misconceptions about mathematics and mathematics learning begin at an early age. Therefore there is a clear need to consider and challenge both personal and community beliefs, attitudes and dispositions about mathematics learning.
Contemporary research about learning and the brain has dispelled many pervasive myths including, but not limited to the:
- gene myth – you either have a maths gene or you don’t
- gender myth – one gender is better than another at maths
- speed myth – ability in mathematics can be measured by how quickly a problem is solved
- memory myth – maths is only about memorising facts, rules and procedures
- perfection myth – mathematicians never make mistakes
- creativity myth – maths is not a creative pursuit as there is usually one right way and one right answer.
One of the best ways we can help children and young people is to promote positive attitudes towards mathematics.
Read
Youthontrack.justice.nsw.gov.au (2019). [online] [accessed 7 Aug. 2019]. for:
- research papers
- reviews of research studies
- technical reports
- conceptual pieces to challenge and dispel common myths about mathematics.
Numeracy in the 21st century
Numeracy has never been more important. The rapidly evolving nature of knowledge, work and technology, demands stronger understanding, reasoning and strategic and problem-solving skills.
To represent the multi-faceted nature of numeracy in the 21st century, Professor Merrilyn Goos developed a model for numeracy in the 21st century (see figure 1) which contains several elements related to numeracy knowledge and behaviours.
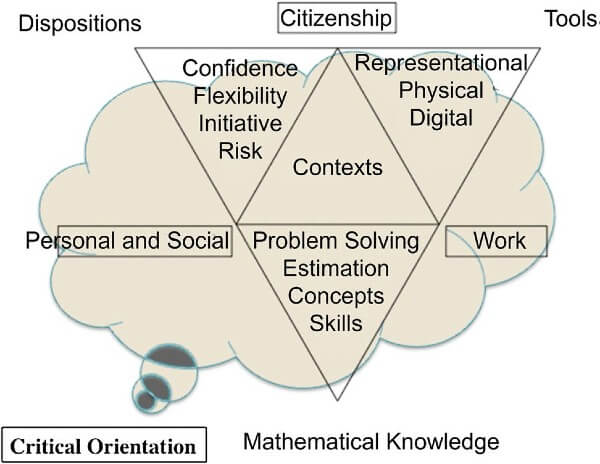 Figure 1: Professor Merrilyn Goos's model for numeracy in the 21st century.
Figure 1: Professor Merrilyn Goos's model for numeracy in the 21st century.1: Long description
This diagram critically orients the viewer into several elements related to numeracy knowledge and behaviours. It depicts a larger upturned equilateral triangle, resting on its apex.
The term, mathematical knowledge is noted on the bottom vertex (apex) of the triangle, the term dispositions on the left vertex of the triangle, and the term tools on the right vertex of the triangle.
The term ‘Personal and Social’ is noted on the left side of this triangle, the term ‘Work’ on the right-hand side and ‘Citizenship’ is noted on the base of the triangle.
This larger equilateral triangle is divided into four smaller, equilateral triangles of equal shape and size. The lower triangle is upturned and contains the terms ‘Problem Solving, Estimation, Concepts and Skills. Above this triangle is a layer of three triangles. The left-hand triangle is upturned and contains the words ‘Confidence, Flexibility, Initiative and Risk’. Adjoining this triangle is another inverted equivalent sized triangle that contains the term ‘Contexts’. On its right is an upturned triangle containing the terms ‘Representational, Physical and Digital’.
The model views numeracy as having the capacity to use mathematical knowledge in a range of contexts, both within schools and beyond school settings:
- to have positive dispositions to maths and the confidence, willingness and preparedness to flexibly use mathematical approaches and knowledge to engage with life-related tasks
- to use physical materials and tools (models, measuring instruments), representations (symbol systems, graphs, maps, diagrams, drawings, tables) and digital tools (computers, software, calculators, internet) to mediate and shape the mathematical actions and thinking.
The model suggests there is a need for a critical orientation that enables the use of mathematical information to make decisions and judgements, and to argue and challenge.
Other frameworks for interpreting numeracy are documented in the research literature. For example, the Numeracy Framework developed by Willis and Hogan (Hogan, 2000) incorporated three types of knowledge:
- Mathematical knowledge – the knowledge needed for intelligent mathematical action
- Contextual knowledge – the ability to link mathematics to experiences
- Strategic knowledge – the ability to ask questions about the application of particular mathematical knowledge.
For more information, visit
Birth to level 10 numeracy guide.
Maths monographs
This research highlights some of the key issues around the teaching of maths and numeracy.
Each monograph in the series provides a summary of the current research around an issue that is impacting Mathematics teaching and learning in schools as well as a range of activities to support reflective consideration of these issues amongst teams of teachers in schools.
The supplementary materials for each monograph provide a selection of activities to support teachers and schools to apply this knowledge to practice individually or in collaboration with colleagues.
Consider using these activities as prompts to discuss one of the monographs in professional learning communities or as a whole school team.
Titles in the series currently include:
-
Mathematics anxiety by Dr Sarah Buckley, Senior Research Fellow, ACER: This research is intended to present information for reflecting on and planning how mathematics anxiety can be reduced and regulated in classrooms and the school community.
-
Critical connections between numeracy and mathematics by Dave Tout, Senior Research Fellow, Numeracy and Mathematics, Tertiary and Vocational Assessment Services, ACER: Increasingly research is showing that life and work in the 21st century is requiring higher levels of mathematics and numeracy of its citizens.
-
Engaging families in mathematics education by Leicha A. Bragg, Sandra Herbert and Jill P. Brown, Senior Lecturers in Mathematics Teacher Education, Deakin University: Fostering school-home partnerships is pivotal in enhancing an inclusive education beyond the classroom, and in turn, supports mathematics learning in the classroom.
-
Gender and Mathematics by Helen Forgasz and Gilah Leder, Monash University: To address the gender differences in mathematics learning outcomes that are found, most often favouring boys and men, it's important to understand the underlying reasons.
-
Teaching mathematics from a cultural perspective by Professor Chris Matthews, University Technology of Sydney: Drawing on personal and professional experience, Professor Chris Matthews argues that a richer mathematics education comes from teaching from a cultural perspective.
-
The STEM agenda by Dianne Siemon Emeritus Professor, RMIT University: In this monograph, Emeritus Professor Di Siemon invites school leaders and teachers to consider the implications of the STEM agenda for the teaching and learning of mathematics at their school in terms of two related issues; access and outcome.
-
 Ability Grouping by Dianne Siemon Emeritus Professor, RMIT University (pdf - 721.45kb): Ability grouping remains one of the most contentious issues in mathematics education today. What is the problem that ‘ability’ grouping seeks to address? How can we organise the teaching and learning of mathematics to support all learners?
Ability Grouping by Dianne Siemon Emeritus Professor, RMIT University (pdf - 721.45kb): Ability grouping remains one of the most contentious issues in mathematics education today. What is the problem that ‘ability’ grouping seeks to address? How can we organise the teaching and learning of mathematics to support all learners?
– Page 18 of the pdf refers to the PowerPoint
Ensure you have downloaded and refer to the accompanying
Ability Grouping Provocation (ppt - 1.4mb) The notion of Big Ideas in mathematics education is not new. What are Big Ideas in school mathematics and why are they important? What implications do Big Ideas have for the teaching and learning of mathematics?
– Page 18 of the pdf refers to the PowerPoint
Evidence for learning toolkits
Teaching and Learning Toolkit
The
Teaching and Learning Toolkit and the Early Childhood Education Toolkit are designed to support teachers, educators and school leaders who are making decisions about how to improve learning outcomes, particularly for children and young people from settings surrounded by disadvantages.
The toolkits do not make definitive claims as to what will work to improve outcomes in a given school. They provide high-quality information about what is likely to be beneficial based on existing evidence.
Early Childhood Education Toolkit
The
Early Childhood Education Toolkit summarises the global research on 12 topics relevant to early childhood education to give children the best chance of success regardless of their background. You can view all approaches in the global evidence base and also examine the Australasian Research Summaries.
Summary of the Australasian research and evidence
A
summary of the Australasian research and evidence on each of the approaches in the Teaching and Learning Toolkit.
References
Mathematics and numeracy
Adoniou, Misty1, Yi, Qing. (2014).
Language, mathematics and English language learners, The Australian Mathematics Teacher, vol 70 Issue 3 [online]
Attard, C. (2017). Opinion. Mathematics education: Who's responsible? The Australian Mathematics Teacher vol. 73 no. 2, 73(2), 3-4.
Boaler, J. (2016).
Mathematical mindsets. San Francisco, CA: Jossey-Bass.
Goos, M., Bennison, A., & Proffitt-White, R. (2018) Sustaining and scaling up research-informed professional development for mathematics teachers. Mathematics teacher Education and Development, 20.2, 133-150
Goos, M., Geiger, V., & Dole, S. (2012). Changing teacher practice through a rich model of numeracy across the curriculum. In Gangnae-Myeon, Cheongwon-Gun, Chungcheongbuk-Do (Eds.), 12th International Congress of Mathematical Education, Seoul, The Republic of Korea, pp. 4329-4337, Korea National University, Republic of Korea: International Congress on Mathematical Education [ICME].
Goos, M., & Jolly, L. (2004). Building partnerships with families and communities to support children’s numeracy learning. In I. Putt, R. Faragher & M. McLean (Eds.), Mathematics education for the third millennium: Towards 2010. Proceedings of the 27th annual conference of the Mathematics Education Research Group of Australasia [MERGA], pp. 279-286. Townsville, QLD: MERGA.
Industry Skills Council. (2018)
No More Excuses.
O'Connor, M., & Thomas, J. (2019).
Australian Secondary Mathematics Teacher Shortfalls: A Deepening Crisis. Australian Mathematical Sciences Institute. Australian Mathematical Sciences Institute. Retrieved June 24, 2019.
Shomos, A., & Forbes, M. (2014). Literacy and Numeracy Skills and Labour Market Outcomes in Australia. Canberra: Productivity Commission Staff working paper.
Tout, D., & Turner, R. (2016). Are Australian Mathematical Foundations Solid Enough for the 21st Century?
ACER Research Conference Proceedings. Melbourne: Australian Council for Educational Research (ACER).
YouCubed. (2019).
Dispelling Myths about Mathematics - YouCubed. [online] [Accessed 29 Jul. 2019].
Woo, E. (2019, May 24). 'Key to human flourishing': how mathematics is shaping our future. The Sydney Morning Herald.
Curriculum
Callingham, R., Beswick, K., Carmichael, C., Geiger, V., Goos, M., Hurrell, D., Hurst, C., Muir, T., (2017). Nothing left to chance. Characteristics of schools successful in mathematics. (Report of the Building an Evidence Base for Best Practice in Mathematics Education Project). Hobart: University of Tasmania.
Department of Education and Training. (2011).
VEYLDF Evidence paper and Practice Guide: High Expectations for Every Child. Retrieved on 24 January 2018.
Dinham, S. (2016). Leading learning and teaching. Melbourne: Australian Council for Educational Research, p.125
Marzano R.J. (2017). Communicating high expectations. In Marzano, R.J. The new art and science of teaching. Cheltenham, Australia: Hawker Brownlow Education.
Morony, W., Hogan, J. & Thornton, S. (2004). ANSN Snapshot: Numeracy Across the Curriculum. Lindfield, New South Wales: Australian National Schools Network.
Steiner, D. (2017) Curriculum Research:
What We Know and Where We Need to Go. Johns Hopkins School of Education. Retrieved August 2019.
YouCubed. (2019).
Dispelling Myths about Mathematics - YouCubed [online] [Accessed 7 Aug. 2019].
Research