Level 5: Proportional Reasoning
Materials
Instructions
Place the counters in front of the student and say, “Can you make a collection where number of blue to yellow counters is in the ratio 3 to 2?” … Note student’s response. If experiencing difficulty, say, “That means three blue counters for every two yellow counters” … Note student’s response. If collection made correctly, ask, “How would you write that? … Can you make another collection where the number of blue counters to yellow counters is still in the ratio of 3:2?” … Note student’s response
Replace counters and ask, “Can you make a collection where the number of yellow to red to blue counters is in the ratio 1 to 3 to 5?”?” … Note student’s response. If collection made and recorded correctly, place 9 red counters in front of the students and ask, “If I wanted to make a collection in the same ratio using 9 red counters, how many yellow and how many blue counters would I need?” … Note student’s response.
Place the Egg Card and Egg Representation Cards in front of the student, point to the large card and say, “This card shows 7 brown eggs and 5 white eggs … Can you tell me how each of these smaller cards relate to the eggs?” … Ask student to explain his/her reasoning for each and note response.
If these tasks completed fairly easily, place the Party Punch Worksheet in front of the student and say, “Please solve these problems using as much mathematics as you can” … Explore student’s thinking, note responses and retain worksheet.
5.6 Advice Rubric
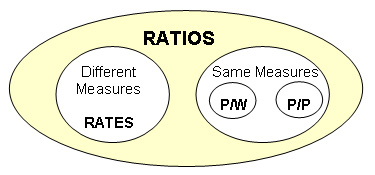
Ratio involves the comparison of any two quantities. For example, ratio can be used to compare the number of people to the size of the room. More specifically, ratio can be used to compare measures of the same type, for example, the number of males compared to the number of females in the room. Within this category, two other types of comparison are possible, for instance, one can compare the parts to the parts (eg, males to females) or the parts to the whole (eg, females to the number of people). Ratios can be also used to compare measures of different types, for example, the number of people per square kilometre. Comparisons of this type are generally referred to as rates. These classifications are shown in the diagram below from Lamon (1999).
This task examines the extent to which students are able to physically represent ratios, recognise ratio equivalents, interpret ratio symbols, and use ratios and/or proportional reasoning to solve missing value problems. It assumes some prior experience with simple ratios.
| Observed response |
Interpretation/Suggested teaching response |
|---|
| Little/no response, may identify some of the symbol cards in relation to the eggs, but unable to solve the missing value problems |
May not understand task or be familiar with ratio expression - Explore student’s knowledge of fractions, decimals, and per cent (see Level 4), review and apply as necessary to build a sense of proportion
- Discuss simple relational situations to identify ‘what is being compared with what’, eg, Is it a ‘then and now’ situation, are parts being compared with other parts or with wholes?
- If appropriate, introduce the idea of ratio and how it is expressed using real-world examples, explore comparisons in terms of parts and whole, (eg, use the Mixing Juices task (pdf - 24.96kb))
|
| Produces BBB YY, may record appropriately but unable to produce alternative representation or represent 1:3:5 collection accurately (eg, ratio correct but colours incorrect), interprets most of the symbol cards in relation to the eggs and makes a start on missing value problems |
Suggests a limited understanding of ratio and how it can be applied to solve problems - Use real-world problems to review the meaning and use of ratio and how it is expressed, link ratios to fractions drawing attention to differences between part to part comparisons and part to whole comparisons (as done for the Egg Card)
- Practice making, naming and recording multiple collections for a given ratio, eg, for 3:5 collections could be represented by 3 blue and 5 red or any common multiple of these such as 6 blue and 10 red
- Explore and discuss solution strategies for missing value problems. Invite students to create similar problems, share and discuss as appropriate
|
| Able to represent and record collections accurately, provides alternative, and recognises the number of yellow and blue counters needed for 9 red counters, interprets symbol cards correctly, solves missing value problems but may rely on fairly cumbersome techniques and strategies and/or make arithmetic errors when more difficult numbers involved |
Suggests a sound understanding of ratio and access to some appropriate strategies, may not generalise to a wider range of problems - Use real-world problems to review the meaning and use of ratio and how it is expressed, link ratios to fractions drawing attention to differences between part to part comparisons and part to whole
- Explore and discuss strategies for solving an expanded range of proportional reasoning problems, particularly ones involving the use of non-integral values
- Consider relating ratios to work on transformations, scale diagrams, variation, inverse proportion, and more complex missing value problems
|