Level 6: Generalising
Materials:
Instructions:
Place scissors and 5 lengths of string in front of the student and ask, “Can you take one piece of string, fold it in half then cut across both strands once? … How many pieces of string do you have?” Ask student to record the result in the table on the String Cutting Record Sheet.
Continue with other pieces of string, making 2, 3, 4, and 5 cuts respectively and recording results in the table.
Ask: “Can you see any patterns in the table? .... Could you describe them for me please?” Note student’s response. “Without cutting any more string, can you use what you know about the patterns to complete the table? …. Can you tell me how you did that please? …
If a general pattern not described in words or symbols, ask, “Is there any way we could tell someone else how many pieces would be made by any number of cuts?” As you say this, indicate the ‘n’ in the remaining top row cell of the table. Note student’s response and explore his/her thinking.
If the general pattern was described fairly quickly in words or symbols, ask: “What do you think might happen if instead of folding the string in half, it was folded into three parts and then cut like before?” … Note student’s response.
6.3 Advice Rudric
Working with number patterns has long been recognised as a means of introducing the notion of variable and more formal algebraic expression. However, there is often a disjunction between the physical models used to illustrate these patterns (eg, matchsticks, tiles, wooded cubes, diagrams etc) and the formal language that is used to describe them in general terms. One of the reasons for this is that students will ‘see’ and therefore ‘count’ physical representations of patterns in different ways. More often than not, these ways are different to the more elegant and efficient ways ‘seen’ by teachers of mathematics and textbooks. In the advice below, reference is made to Max’s Matchsticks (pdf - 27.6kb), which encourages students and teachers to see that patterns can be viewed and described in different ways. Connecting pattern descriptions to how the elements might be counted is important as many students believe that finding ‘the’ rule is a matter of guesswork or something that should just ‘pop’ into one’s head. In this task, the different strategies lead to different general descriptions (see below) which can be used to show equivalence and as a basis for a discussion about elegance and simplicity which justifies why one expression of the rule might be preferred over others.
Student responses to this task indicate the extent to which they are able to recognise, use, and describe a simple number pattern.
| Observed response |
Interpretation/Suggested teaching response |
|---|
| Notices that the number of pieces of string ‘goes up by 2’ with each cut, unable to say how many after 20 cuts without modelling and counting all or listing all elements in the sequence |
Recognises difference between sequential terms but experiences difficulty describing functional relationships - Use idea of ‘input/output machine’ and simple rules such as doubling, doubling and 1 more, take 3, squaring, and so on to establish the idea of a general rule and how it works
- Invite students to create a partial table of values for their own ‘secret’ rule to play ‘guess my rule’ with peers
- Use Max’s Matchsticks (pdf - 27.6kb) to acknowledge that people ‘see’ patterns in different but ultimately equivalent ways.
- As a follow-up to Max’s Matchsticks, invite students to express the various strategies in words but referring to ‘the number of squares’, eg, for Jo’s strategy, which counted the number of matches/square then subtracted the ones that had been double-counted, this might be “4 times the number of squares minus 1 less than the number of squares”
- Talk about what stays the same and what is different and develop general expressions for each strategy (eg, for Jo’s strategy this would be 4 × n – 9 or 4n – 9). Compare strategies and establish their equivalence. Discuss issue of elegance and simplicity and why 3n + 1 might be the preferred representation of this pattern
|
| Notices that the number of pieces of string increases by 2 with each cut, able to complete the table for 21 pieces of string (10) and 20 cuts (41) and describe pattern in words, may not be able to apply for 237 pieces of string or comment appropriately on what will happen when string folded in 3 parts |
Able to describe simple patterns in natural language (eg, double the number of cuts plus one), may not be able to describe more generally or use accurately - Use Max’s Matchsticks activity (if not already used) to review the process of constructing general rules (ie, from counting ‘rules’ for particular cases to the general by identifying what stays the same and what changes and expressing this in words)
- Use other matchstick patterns to explore different strategies and rule generation, eg,
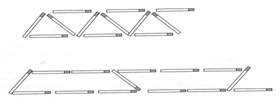
- Building block patterns can also be used to explore rule generation and application
- Investigate more general problems which can be explored diagrammatically, eg, Is there any way of determining the number of diagonals for an n-sided polygon?
- Use rental situations where a certain amount is paid and then an hourly or kilometre rate is charged to show how generalised ‘rules’ might be applied in the ‘real-world’
|
| Able to complete the table, states general rule in words and/or symbols, identifies what will happen when 3 pieces of string are cut (3n + 1) in words and/or symbols |
Suggests a sound understanding of linear patterns and a capacity to use algebraic text in this context - Consider introducing pattern identification activities involving non-linear relationships, eg, Super Packer (pdf - 30.16kb), and growth/decay patterns (see Maths300)
- Explore the value and power of algebraic text in different contexts, eg, to problems such as, The street numbers of 4 houses add to 3196. What are the numbers? Discuss assumptions and problem representation
- Extend to problems involving non-linear relationships, eg, 365 is an extraordinary number. It is the sum of 3 consecutive square numbers and also the sum of the next two square numbers. Find the numbers referred to.
|