Level 4: Partitioning
Materials
Instructions
Place the Equal Parts cards in front of student and say, “All of these squares and circles have been divided into 4 parts. Which ones are fractions? If not done spontaneously, suggest student places the cards into two groups. Note student’s response and ask them to explain their reasoning by asking why cards were placed in each pile, eg, fraction cards are:
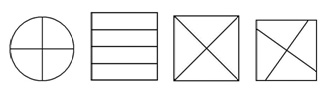
If at least 2 cards correctly identified as showing fractions, place the top half of the worksheet in front of the student and say, “Can you shade this rectangle to show 2 fifths please? ... Can you tell me why you did it that way?” Note student’s strategy. If student appears hesitant, ask, “What seems to be the problem here?” Note student’s response.
Place the bottom half of worksheet in front of the student and say, “Can you shade this rectangle to show 2 fifths please? ... Can you tell me why you did it that way?” Note student’s strategy. If student appears hesitant, ask, “What seems to be the problem here?” Note student’s response.
4.1 Advice rubric
Although it is commonly assumed that Year 2 to Year 4 students ‘see’ what most adults ‘see’ in fraction diagrams, this is not generally the case. Indeed, many students do not look at the relevant attribute of area, but at the lines, vertices and shapes represented. This is not surprising given that for the past 3 to 6 years, they have been asked to focus on these attributes to recognise the properties of two dimensional shapes. Recent research suggests that even though students may correctly solve fraction problems (eg, If 3 pizzas are shared among 4 people, what fraction of pizza will each person receive?), they are unable to recognise or draw a correct representation of this (SNMY, 2005).
This task is designed to evaluate the extent to which students’ recognise the importance of equal parts in fraction representations.
| Observed response |
Interpretation/Suggested teaching response |
|---|
Little/no response |
May not understand task
- Use plasticine or play-dough to make recognised wholes (eg, a ‘pizza’, rectangular ‘cake’ or ‘sausage’) cut as appropriate to distinguish between equal parts and unequal parts, emphasising that those with equal parts show fractions. Use models to make and name fractions.
- Extend to paper-folding, creating equal and unequal parts to distinguish between fraction and non-fraction models, and link paper models to diagrams.
|
Identifies at least some fraction cards correctly but includes the following card
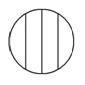
May attempt to shade 2 fifths but likely to do this without reference to the number (6) or nature (unequal) of the parts |
Suggests equal parts recognised to some extent but can be over-ridden by strong, misleading perceptual information
- Investigate ‘fair shares’ using a variety of physical models (eg, plasticine, paper, streamers, ‘Smarties’), discuss relevant attribute (eg, area or length) and explore ways in which equality of parts can be tested (eg, cut up and laid on top of one another)
- Consider introducing halving and thirding partitioning strategies via paper-folding (see Partitioning (PDF - 215Kb) (pdf - 199.51kb) paper) with a view to scaffolding students’ capacity to generate their own fraction models and diagrams.
|
Identifies 3 fraction cards but not the following:
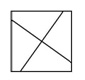
Some attempt to shade 2 fifths, recognises at least one issue making this difficult (ie, the number and/or nature of parts), eg, may eliminate one part from the first diagram or guess to estimate 2 fifths. |
Suggests equal parts recognised to some extent and some awareness of the importance of the number of parts
- Investigate ‘fair shares’ as above, extend to non-conventional representations such as the one shown here and the means by which these can be tested (see above)
- Introduce/consolidate halving and thirding partitioning strategies (see above)
- Consider introducing fifthing strategy (see Partitioning (PDF - 215Kb) (pdf - 199.51kb) paper) using a variety of materials.
|
Identifies all fraction cards and recognises that both the number of parts (first diagram) and the equality of the parts (second diagram) are problematic, may attempt to deal with these in some way |
Recognises the importance of equal parts and the total number of parts irrespective of representation
- Extend the use of the halving, thirding and fifthing partitioning strategies (see Partitioning (PDF - 215Kb) (pdf - 199.51kb) paper) to expand students’ capacity to generate their own fraction models and diagrams irrespective of representation.
|
Identifies all fraction cards correctly and shades to show 2 fifths fairly accurately (ie, slightly more than 2 sixths for the first diagram and to the mid-point of the third part for the second diagram) |
Suggests access to meaningful partitioning strategies and an understanding of how fractions are named and represented
- If not already recognised, make partitioning strategies explicit and use to make and name a wider range of fractions using region diagrams and open number lines (eg, tenths, twelfths, fifteenths etc)
- Use partitioning strategies to re-name common fractions, developing the generalisation: If the total number of parts is increased by a certain factor, then the parts shaded or required are increased by the same factor.
- Consider introducing/consolidating decimal fractions to thousandths by successively ‘tenthing’, use to compare, order, sequence and rename decimal fractions
|