The following beliefs and/or practices would be fairly widely recognised by most teachers of mathematics:
- multiplication makes larger, division makes smaller
- when subtracting by place-value parts, find the difference
- when multiplying (or dividing) by powers of 10, zeros are ‘added’ or ‘crossed off’ to find the answer
- the larger the numerator or denominator, the larger the fraction (conversely, the smaller the numerator or denominator the smaller the fraction)
- the longer the string of decimal fraction parts the larger (or smaller) the number
- when adding/subtracting fractions, you add/subtract denominators on the grounds that ‘what you do to the top, you do to the bottom’
- when multiplying or dividing decimal numbers by powers of ten the decimal point moves to the right or left
- the tenths, hundredths, thousandths etc live to the left of 0 on the number line
- when dividing you don’t need to record 0 as it means nothing (138 recorded as the answer to 6540 divided by 5)
- to change a fraction into a decimal, multiply by 100 over 1
- two negatives make a positive.
While some of these might be regarded as ‘misconceptions’ and others as ‘helpful rules’ introduced by teachers and/or texts, they have two things in common. They both work some, if not all, of the time depending on the particular context in which they are exercised, and they both serve to reinforce the view that school mathematics is about learning and applying fairly meaningless rules or procedures.
A Thesaurus search on ‘misunderstandings’ produces: “mistakes, quarrels, mix ups, errors, misconstructions, confusion, misinterpretations, misapprehensions…”.
A search on ‘misunderstand’ produces: “get the wrong idea, misinterpret, misconstrue, get the wrong impression, misread, misapprehend”.
Of these, ‘misconceptions’ is probably the term that has been used most widely in the mathematics and science education literature, however, its use has declined in recent years with the recognition that individuals do not construct meaning in isolation from their socio-cultural setting.
No-one sets out to invent a misconception or misconstrue their experience. Individuals make sense of their experience, shared or otherwise, on the basis of what they already know or attend to in the moment, and what is seen to be valued by the community in which the experience is situated.
That is, on the basis of what represents a ‘best fit’ in the circumstances. In this sense, there is an argument that there are no such things as misconceptions, just
alternative conceptions that are as good as they can be given the student’s prior knowledge and their opportunities to learn.
For example:
| A common misunderstanding |
|---|
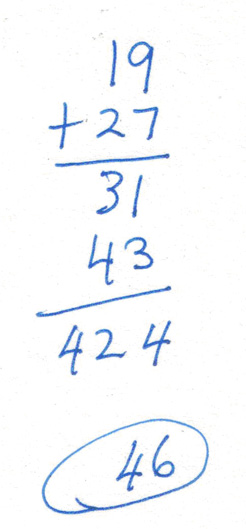
Richard (not his real name) used this method to add 19 and 27. In Year 5 at the time, Richard was known to have considerable difficulties with place-value. His reasoning here was identified by his teacher who knew that Richard was an avid AFL fan.
Unable or lacking the necessary confidence to work with the base ten number system, Richard applied what he did know, rewriting the numbers in terms of football scores: 19 points is 3 goals and 1 behind, 27 points is 4 goals and 3 behinds.
Adding goals, he then recorded 42, on the grounds that 7 goals is 42 points, and 4 as the sum of the behinds. Consistent with football scoring he then added the 42 points and 4 behinds to arrive at his answer of 46. |
 |
This is an alternative conception rather than a misconception. While the analysis identifies a starting point for teaching, this should not be the only response to Richard’s work sample. The classroom practices that, over time and to various extents, have contributed to this state of affairs also need to be addressed.
Another important point to remember from a social constructivist perspective is that errors may not indicate misconceptions. For example, a Year 4 student gave the following response to the problem, 8 families shared a lottery win of $348, how much did each family receive?

Nick (not his real name) had previously demonstrated that he could quickly and accurately solve division problems like this using
guzinta (that is, “8 goes into 3 … no, 8 goes into 34 … yes, 4 times and 2 over …8 goes into 28 … yes, 3 times and 4 left over”).
Challenged in class over a period of three weeks to shift to a partitive approach using MAB materials, Nick demonstrated that he could physically share the materials and confidently use the related language (that is, “3 hundreds shared among 8? … no, rename as tens, 34 tens shared among 8? … yes, 4 tens each and 2 tens remaining, rename as ones … 28 ones shared among 8? … yes, 3 ones each and 4 left to share”).
However, when asked to solve this word problem some time later, Nick chose to create his own algorithm based on what he knew about subtraction and renaming. In this case, reading from the top down and starting with the ones he reasoned, “8 how many 8s? … 1 … 4 how many 8s? Can’t do, so trade a hundred, 14 tens how many 8s? …1 and 6 over”, which he records over the 2 in the hundreds place.
Realising “2 how many 8s?” is not going to work, he crosses the 6 out and rewrites the 2 and the 6 as 26 and proceeds, “26 how many 8s? … 3 and 2 remainder” which he records.
His comments indicate his beliefs about what he sees school mathematics is about, that is, using ‘sums’ to get answers.
When asked about his answer, Nick, said, “Oh if it was real money I wouldn’t do it like that”. Prompted to say how he would do it, Nick replied, “Well 8 families, $40 each that’d be $320, $50 each would be $400, I reckon it’s about $43”.
Nick’s problem was not with division but with the values and beliefs he held about the nature and purpose of school mathematics. Asked why he did this, Nick said that, he knew his “old way of doing it would work but Mrs ... didn’t like that” and he could do the new way “but that was too long.”
These considerations are important because they broaden the focus of attention from the individual who has an alternative conception, to the ‘big ideas’ and learning environments that are needed by all students to support further learning with understanding.